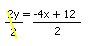To start off class, Ms. Armstrong talked about a math event starting some time in April. It's the Galois Contest for Grade 10 Mathematics.
*If anyone's interested, please let Ms. Armstrong know.

Today in class, we didn't write any notes or do any assignments. Our unit, "Analytic Geometry" is now over. The next unit that we're doing is called, "Exponents and Radicals."

Hey Gummy Bears,
Ever wonder where people are when they check out our blog?? Now you can know. I've put a visitor map at the bottom of the home screen. Let's see how many different countries are represented by the end of the semester.
Ms. Armstrong

Hello Gummy Bears,

y=-2x +3
3
y=-2x -1 These lines are all parallel. They all have the same slope (m).
3
y=-2x+o (Remember y = mx + b)
3









Perpendicular Lines:
-->have negative reciprocal slopes.

*Remember that the perpendicular lines meet to form right angles.

Here is an example of a graped perpendicular lines:

I hope this all make sense ....becuase I did my best ...!! Gudluck to the next blogger........haha!!
The next bLogger is TAN!!

Hello Gummy Bears,

Last week, we were taught how to graph an line using a table of values, how graph a line using intercepts and how to graph a line using the slope-intercept method.

Today, we learned how to find the equation of a line. There are questions that will help us in doing this.

• What are you asked to find?


• What do you know?


• What can you do with that info?


• Anything else?

Now, we will find the equation on this line:

In solving this, we'll use the questions above.

Now that we know that y=1/3x+1, we can plot other points. Always remember that the distance for every point in the line is the same.

If you want to find the equation of a line and you are NOT given the the y-intercept but you have the coordinates of a pt. and the slope, you can still find the equation.

another example:

1. points are (-1, 4) and m=-1/3

m=(x-x1)=y-y1

1/39-1=-x=4+-y

-1/3 - 1/3x=4-y

[4-1/3]-1/3x=y

11/3-1/3x=y

y=-1/3x+11/3

I hope you understand the lesson... I tried really hard on doing this..

If I have mistakes, please inform me and I will correct it...

The next blogger is JAEBY!!!!

Hello Gummy Bears

































Since you are going to be multiplying your x-values by a fraction, it is simplest to pick x-values that are multiples of 3, so the denominator will cancel out.





Here's the T-chart...



...and here's the graph:





*Graph –3x = 6y – 2

Hello there Gummy Bears!!!

Today, instead of the usual lectures, we are told to play a game using strings and pieces of tape. The game required us (in pairs) to graph a line in the “huge coordinate plane floor” using only the slope given.

Again, don’t forget the formula: rise/run


For example: The given slope is ½. To graph a linear equation, we use the slope given to make a line perpendicular to it. Locate the rise which is +1 and then locate the run which is +2.




Now we can draw the line through the points. Since I am finding it quite difficult to emphasize the different points on this graph, I am giving you the liberty to do it by yourselves.

You can easily illustrate the slope on the graph, depending on the information you have about the line and the equation.


Having used most of our time today in playing the game, I would like to share some things about the topic from my browsing. Many people describe "slope" as a measure of the "steepness" of a line. Look at the two graphs below. Which line has a larger slope? Which line appears to be steeper? Explain what is happening.






Solution:
Graph A has a larger slope, even though graph B appears steeper. This appearance is caused by the different scale used in the two graphs. If it were placed on the other scale, the line in graph B would appear nearly flat!


I have also added a great video in case you didn’t fully understand what I’m trying to tell here…

Finally, I was able to do something for my assigned task today BUT I am not sure whether I did justice to it. Hahaha…..


And now, it’s my turn to pass on the TORCH. Choosing…thinking whom to choose…
Finally, the next blogger will be Ian!!!

What comes into your mind when you see the word slope? We think of mountains, the roof of our houses,diagonal lines,or the slides in the playground. But what does slope really mean?

SLOPES are lines that are not in horizontal position. It has an inclined angle. A SLOPE OF A LINE refers to its steepness and direction. Here's an example...









The formula for SLOPE is:





whereas:

RISE - the difference of Ys
RUN - the difference of Xs





Here is problem #1 and it's solution







The NOTATION of the slope is m

remember our previous topic about slope intercept form?



if m = 0 that means that the slope is a horizontal line
if m > 0 that means that the line is diagonal and it rises to the right
if m is less than zerovalue and it goes downward to the right
and if m is undefined or when the fraction has a zero(0) as the denominator, that means that the line is vertical.

next example...

One more example and solution

we were asked to do ex. 7 and 8 (#5-#7)
whew!! I'm done at last!! haha.. well.. hope i did this ryt... did i?

by the way.. sorry for the graphics.. if it doesn't fit.. haha.. if i would reduce its size,, some of the writings would be very small and you wouldn't be able to read it.. so that's it..so sleepy now..

well.. who would be the next blogger?... hmm..let's see.. Arianne? Jaeby? Anthony? David? or Ian? hmm...

tantararan!!! (drum roll..) hahaha.. it's payback time....
ANTHONY!!!

you're nexT!!! haha... (--,)

T.O.V --> first of three ways to graph
In order to graph from a T.O.V the equation must be in slope intercept form.

1. A x + B y + C = 0
A, B, C are integers

eg. 7x + 3y -6 = 0
standard form